Simpson’s Rule Calculator & Simpson’s Rule Formula

Simpson’s Rule Calculator is a mathematical method for approximating the aggregate of a function between two limits, a and b. It’s based on understanding the area under a parabola, or a flat curve. In this Rule, N is an even number and h = (b – a) / N. The y values are the function estimated at equally spaced x values within a and b.

n the numerical study, Simpson’s method is a method for statistical integration, the numerical approximation of specific integrals. Clearly, it is the following approximation for values surrounding equally spaced subdivisions:

Who invented Simpson’s rule?

Thomas Simpson FRS

Thomas Simpson FRS (20 August 1710 – 14 May 1761) was a British mathematician and inventor known for the eponymous Simpson’s rule to approximate definite integrals.

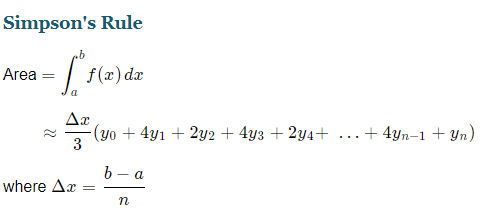
Where does the Simpsons rule come from?

Simpson’s Rule is a numerical method that approximates the value of a definite integral by using quadratic functions. This method is named after the English mathematician Thomas Simpson (1710−1761).

How accurate is Simpson’s rule?

Simpson’s 3/8 rule

Thus, the 3/8 rule is about twice as accurate as the standard method, but it uses one more function value.

SOLUTION

Your input: approximate the integral using rectangles.

Simpson's Rule & Numerical Integration - YouTube

How accurate is Simpson’s rule?

Simpson’s 3/8 rule

Thus, the 3/8 rule is about twice as accurate as the standard method, but it uses one more function value.

What is Simpson’s 1/3rd rule?

In numerical analysis, Simpson’s 1/3 rule is a method for numerical approximation of definite integrals. Specifically, it is the following approximation: In Simpson’s 1/3 Rule, we use parabolas to approximate each part of the curve.We divide. the area into n equal segments of width Δx.

What is Composite Simpson’s rule?

Composite Simpson’s rule

Simpson’s rule is then applied to each subinterval, with the results being summed to produce an approximation for the integral over the entire interval. This sort of approach is termed the composite Simpson’s rule. Suppose that the interval is split up into sub-intervals, with an even number.

What is the order of error in the Simpson rule?

Thus O(h2) for the composite rule, and no asymptotic error for the simple rule. Since the (composite) Simpson rule can be seen as Richardson extrapolation (first step of the Romberg method) of the symmetric trapezoidal rule, its error order is automatically O(h4).

What is the difference between the trapezoidal rule and Simpson’s rule?

The midpoint rule approximates the definite integral using rectangular regions whereas the trapezoidal rule approximates the definite integral using trapezoidal approximations. Simpsons rule approximates the definite integral by first approximating the original function using piecewise quadratic functions.

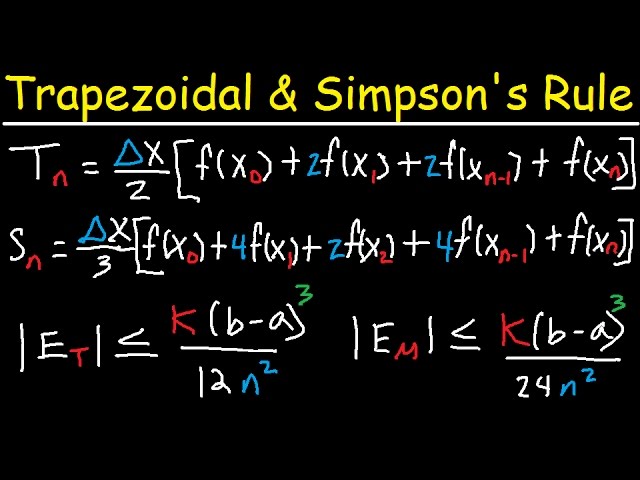
Is Simpson or trapezoidal better?

In trapezoidal we take every interval as it is. In simpson’s we further divide it into 2 parts and then apply the formula. Hence Simpson’s is more precise.

Why is Simpson’s rule more accurate?

We seek an even better approximation for the area under a curve. In Simpsons Rule, we will use parabolas to approximate each part of the curve. This proves to be very efficient since it’s generally more accurate than the other numerical methods we’ve seen. (See more about Parabolas.)

Now, we just evaluate the function at these endpoints:

$f (x_{0}) = f (a) = f (0) = \frac{7^{\frac{2}{3}}}{7} = 0.52275795857471$

$f (x_{0}) = f (a) = f (0) = \frac{7^{\frac{2}{3}}}{7} = 0.52275795857471$ [Math Processing Error]

$4 f (x_{1}) = 4 f (\frac{1}{4}) = \frac{32}{7169} \sqrt[3]{2} {(7169)}^{\frac{2}{3}} = 2.09093460413808$

$4 f (x_{1}) = 4 f (\frac{1}{4}) = \frac{32}{7169} \sqrt[3]{2} {(7169)}^{\frac{2}{3}} = 2.09093460413808$ [Math Processing Error]

$2 f (x_{2}) = 2 f (\frac{1}{2}) = \frac{4}{15} \sqrt[3]{15} \cdot 2^{\frac{2}{3}} = 1.0439647043117$

$4 f (x_{3}) = 4 f (\frac{3}{4}) = \frac{32}{7411} \sqrt[3]{2} {(7411)}^{\frac{2}{3}} = 2.06792304223835$

$f (x_{4}) = f (b) = f (1) = \frac{1}{2} = 0.5$

Related Calculator

CM to Inches