An online synthetic division calculator will allow you to determine the reminder and quotient of polynomials using the synthetic division method. It also finds the zeros of the denominator and the coefficient of the numerator.
In algebra mathematics, synthetic division is the way used to manually perform the Euclidean division of polynomials. The polynomials division also can solve with the long division method. But in the synthetic division, we need short writing and calculation for the answer. So, the synthetic division is the shortest method of the polynomial.
Here we discuss both methods in detail using examples.
What is Synthetic Division?
Synthetic division is a technique used to solve the division operation on polynomials when the division is a linear factor. Its benefit is it allows one to calculate without variables during performing polynomial division, So this is an easy method compared to long division
We can represent the division of two polynomials in the form:
p(x)/q(x) = Q(x) + R/(q(x))
where,
- p(x) is the dividend
- q(x) is the linear divisor
- Q(x) is quotient
- R is remainder
Synthetic Division of Polynomials Definition
When we divide a polynomial p(x) by a linear factor (x – a) (which is a polynomial of degree 1), Q(x) is the quotient polynomial and R is the remainder.
p(x)/q(x) = p(x)/(x- a) = Quotient + (Remainder/(x – a))
p(x)/(x – a) = Q(x) + (R/(x – a))
The coefficients of p(x) are taken and divided by the zero of the linear factor.
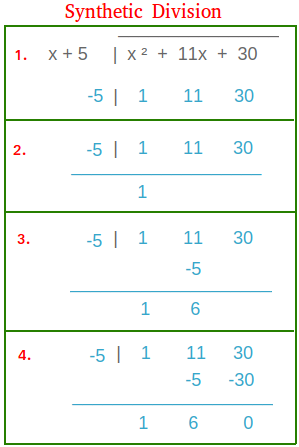
We use synthetic division in the context of the evaluation of the polynomials by the remainder theorem, wherein we evaluate the value of p(x) at “a” while dividing (p(x)/(x – a)). To find if “a” is the factor of the polynomial p(x), use the synthetic division to find the remainder fast. Let us comprehend this better using the example given below
Are you looking for an easy way to solve polynomial equations? Our online synthetic division calculator can help! This method is designed to make long divisions easier, quicker and more efficient so that complicated problems become a breeze – get the answers with just one click. Our mission is to simplify and explain the information we have, and that wouldn’t be possible without our incredible sponsor. We are deeply grateful for their support in making this happen and we want to recommend to you a platform from this sponsor, where you will experience the thrills of what does roulette payout – one of the most iconic table games in gambling! With a great variety of options, it’s no wonder that this classic game is still as popular today. Whether you’re playing on your computer or mobile device, take advantage of its easy accessibility to explore what makes roulette so special for yourself. Discover all that comes with hundreds upon hundreds of trustworthy casinos offering amazing payouts – why not get started now?
